【小学2年生・算数】(7)100より大きい数(~1000まで)
※算数や国語は、地域や同じ区内でも学校によって習う順番や進み具合に違いがあります。
1学期の「長さ」の学習の次に「100より大きい数」について学習をします。
1年生の時は「100までの数」と少しだけ100より大きい数について学習しました。2年生では、「100~1000」くらいまでの数についての学習を行います。
【例題1】イラストの子供たちは全部で何人いるでしょうか?

このようにたくさん人がいる場合は、どのように数えていくと良いでしょうか?
まず、数えやすくするためにキリの良い「10人ずつ」線で囲んでみます。

このようにしていくと「10人ずつの集まり」がいくつか出来ました。


10人ずつの集まりが全部で「24」あります。
そして、イラストの左上の方に10人ずつの集まりで数えられなかった人数が「5人」いるので、それを忘れないようにしておきます。

次に「10の集まりが10個集まると100になる」ので、「100のかたまりが幾つ出来るか」を数えてみたいと思います。
イラストでは「10人の集まり」が「24」ありました。
この「24」を「10と10と4」に分けることで「10人の集まりが10+10の20」と「残り10人の集まりが4つ」あることが分かります。
「10人の集まりが10個で100人」になりますので、ここでは「100人の集まりが2つ」出来たことになります。100人の集まりが2つで「200人」になります。

他には何人いるでしょうか?
「10人の集まりが4つで40人」と、最初に10人ずつ丸で囲んだ時に余った「5人」がいます。

このイラストを基にしてブロック図で表してみると以下のようになります。
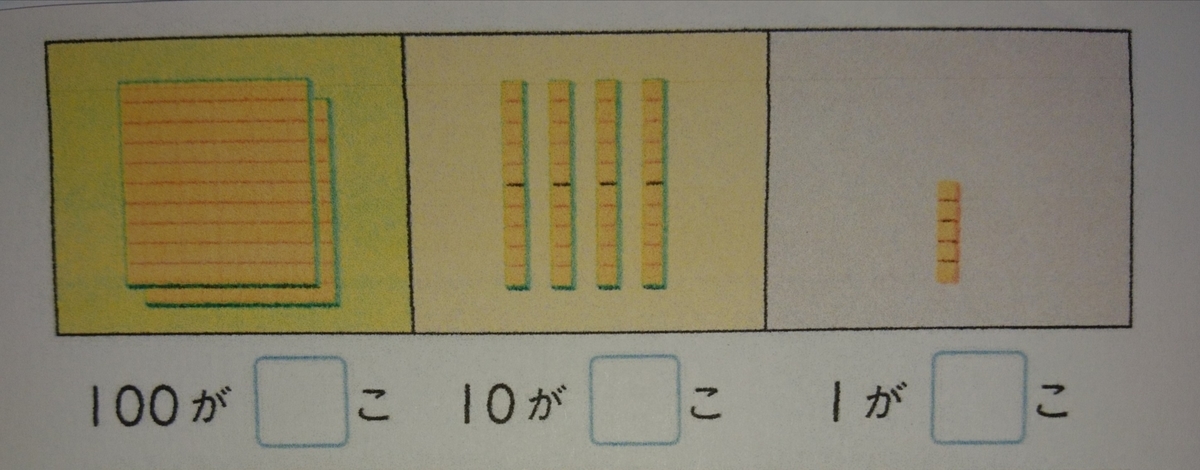
ブロックは「100のかたまりが2つ」と「10のかたまりが4つ」「1が5つ」になります。

ここにある100を2つ集めた数を「二百(にひゃく)」といい「200」と書きます。
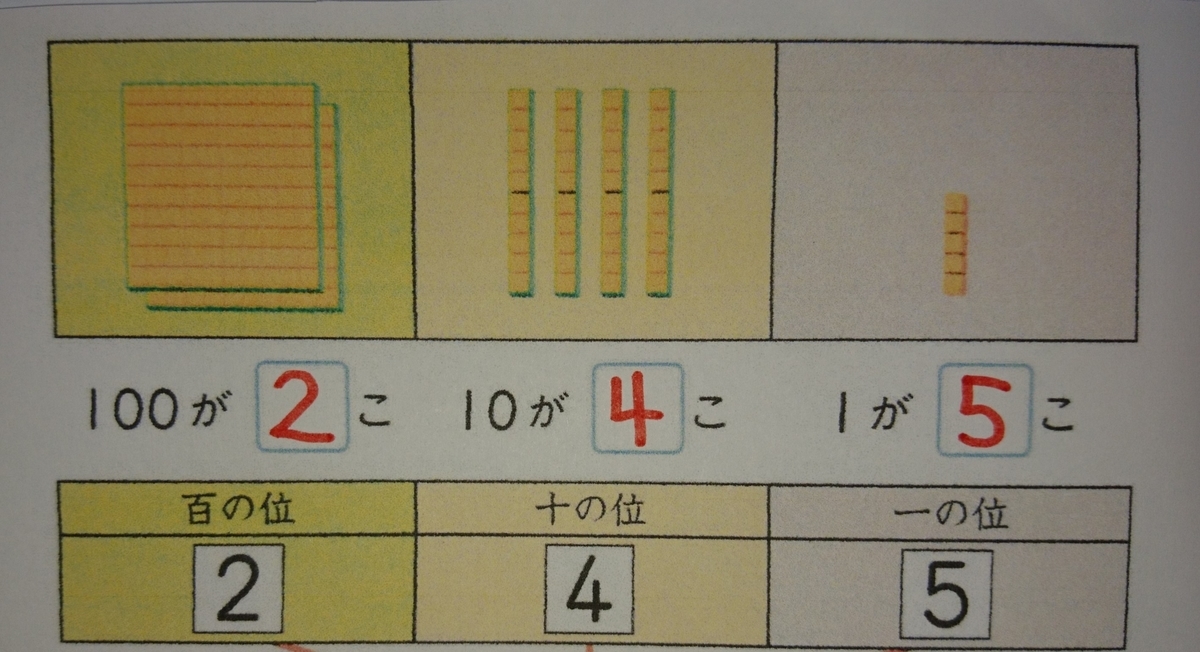
「百の位が”2”」「十の位が”4”」「一の位が”5”」で「245」となり漢数字で表すと「二百四十五」となり「にひゃく よんじゅう ご」と読みます。

これにより【例題1】の答えは子供たちの人数は「245人」となります。
小学生低学年の算数では数字 → 漢数字に、漢数字 → 数字に変換する問題が出たりしますので、どちらの読み方も書き方も出来るようにしておくと良いと思います (#^^#)
例えば上記の「245」は漢数字で「二百四十五」と書き「にひゃく よんじゅう ご」と読みます。
他にも「361」は「三百六十一」と書き「さんびゃく ろくじゅう いち」と読みます。
逆に「七百二十八」は「ななひゃく にじゅう はち」と読み、数字では「721」となります。
※テストでは以下のような問題が出題されることがあります※
【問1】次の数を読みましょう。
(1)296 → 答え:二百九十六
(2)518 → 答え: 五百十八
(3)三百七十四 → 答え:374
(4)六百二十二 → 答え:622
【問2】100を2個と、10を5個と、1を3個合わせた数を書きましょう。
答え:253(または二百五十三)
【例題2】次の折り紙は全部で何枚あるでしょうか?
折り紙のイラストがあります。全部で何枚あるか数えてみましょう。

イラストを見ると「100枚の束」と「10枚の束」それに「1枚ずつ」の折り紙があるのが分かります。
それぞれ幾つあるか数えてみましょう。
「100枚の束」は 「4つ」あります。→ 100が4つで「400」
「10枚の束」は「2つ」あります。 → 10が2つで「20」
最後に「1枚ずつ」が「3枚分」あります。 → 1が3つで「3」
となります。
これを合わせると「400枚」+「20枚」+「3枚」=合計「423枚」となりますので、【例題2】の答えは折り紙は全部で「423枚」となりました。
【例題3】ヒヨコは全部で何羽いるでしょうか?

上記のイラストは1つのブロックにヒヨコが「100羽」います。

100羽のヒヨコのブロックが幾つあるでしょうか?

100羽のブロックが全部で「9個」あります。
しかし、一番右端の下のブロックは1羽だけヒヨコがいません。
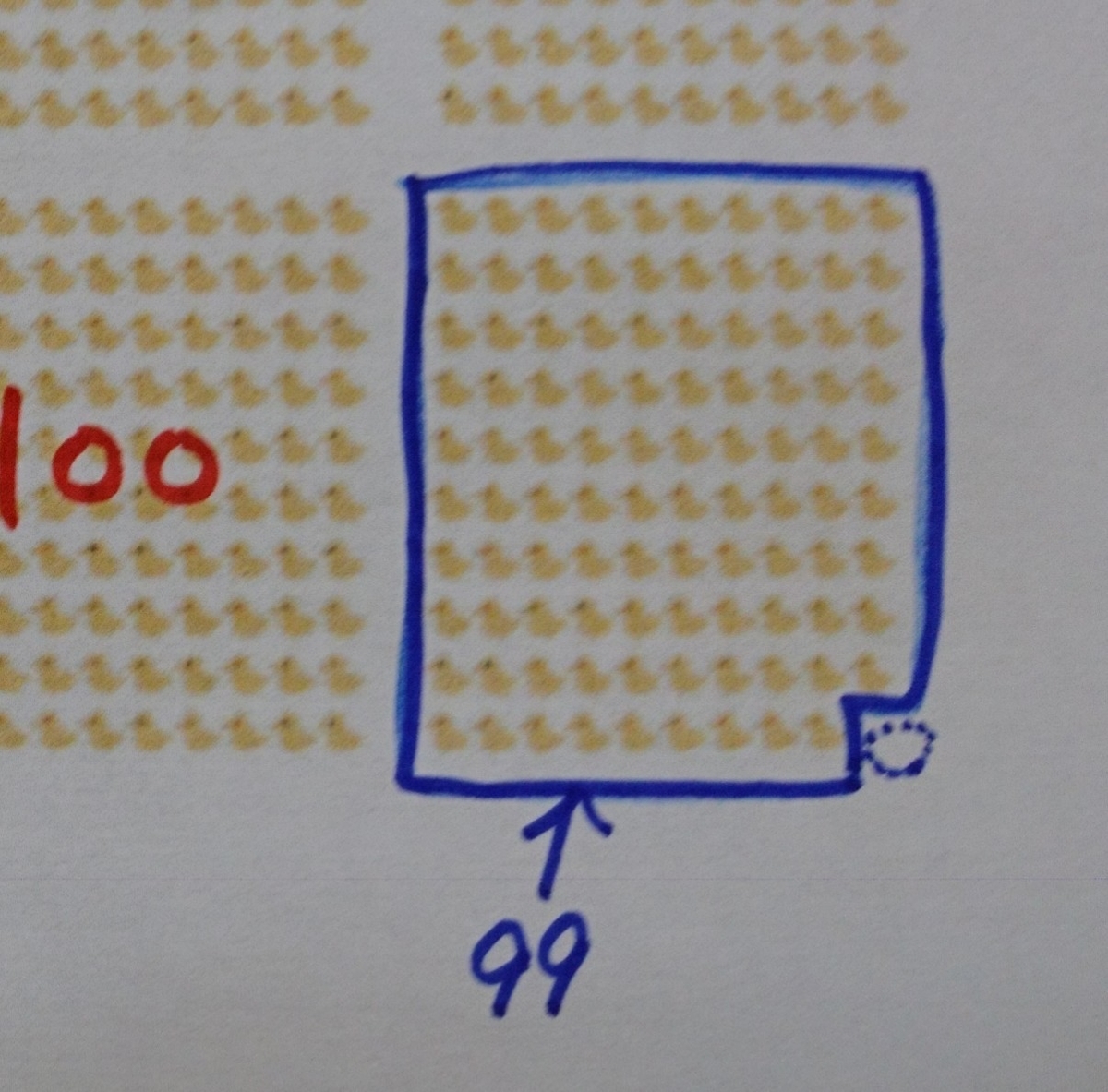
つまり、最後のブロックはヒヨコの数が「100羽より1羽少ない99羽」という事になります。
つまり【例題】のイラストではヒヨコ100羽が集まっているブロックが9つ、それに99羽のブロックが1つという事が読み取れます。
100羽の集まりが9個で「900」、99羽の集まりが1つで「99」となり「900+99=999」となりヒヨコの総数は「999羽」となります。
では、ここに「1羽」ヒヨコが増えたら、全部で何羽になるでしょうか?
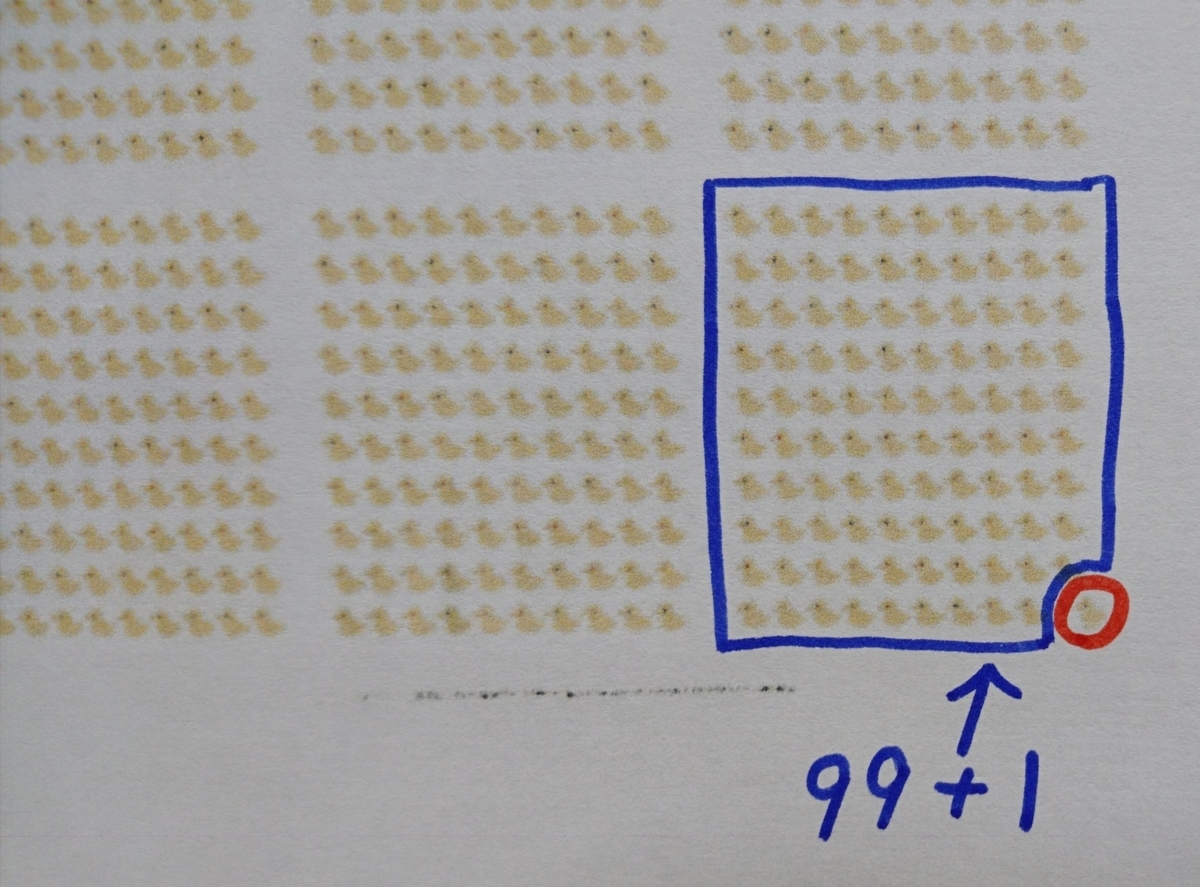
「99羽」に「1羽」増えると「99+1」で「100羽」になります。
もともと「ヒヨコ100羽の集まり」のブロックは「9個」ありました。
そこに「1羽増えて100羽になった集まりのブロックが1つ増えた」という事になります。
「ヒヨコ100羽の集まり」が「9個」→「10個」になったという訳です。
つまり「100のまとまりが10ある」という事になります。

※「100」を「10個」集めた数を「千(せん)」と言い「1000」と書きます。
つまり、ここでは1羽増えたことによりヒヨコの数が「1000羽」になりました。
「1000」は「999より1大きい数」という事になります。
【問1】1000より10小さい数は幾つになるでしょうか?
→ 10小さい数という事は「1000-10=?」になりますので、答えは「990」になります。
【問2】1000より100小さい数は幾つになるのでしょうか?
→ 1000は100が10個分ですので、100小さい数とは「100が9個分」と同じになります。数式は「1000-100=?」となりますので、答えは「900」になります。
【問3】1000は「10を何個」集めた数でしょうか?
→ 「10が10個」で「100」
→ 「100が10個」で「1000」になりますので、「”10が10個”が”10個分”」という事になり、答えは「100個」集めた数になります。
このように大きい数での計算問題も解けるようになっておくと良いです。
【問1】100+200=? → 答え「300」
【問2】400+400=? → 答え「800」
【問3】1000-200=? → 答え「800」
【問4】850-50=? → 答え「800」
大きい数でのたし算・ひき算も今まで学習してきた計算問題と考え方は同じです。
計算問題は毎日数問ずつでも継続的に問題を解く習慣をつけられるようにしておくと良いかと思います (*^^*)